2.6 KiB
Beaterkennung
Die erste von zwei Animationen besteht aus einer Welle, welche von jedem zweiten beat bis zum jeweils nächten beat von oben nach unten läuft. Dafür muss zu jedem Zeitpunkt sowohl die Frequenz als auch die Phase des beats bekannt sein, und das auch über kürzere Störungen oder komplexere Rythmen hinweg.
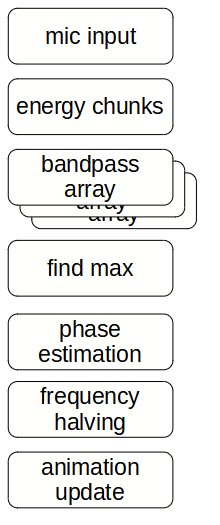
Die zentrale Idee des Algorithmus ist es, Bandpassfilter mit schwacher Dämpfung als Phasenschätzer zu missbrauchen. Hierfür wird eine ganze Reihe an Bandpässen mit unterschiedlichen Durchlassfrequenzen parallel geschaltet. Diese Durchlassfrequenzen gehören zu unterschiedlichen beat-Geschwindigkeiten. In unserem Fall von 105 bis 150bpm, weil sich hier die elektronische Tanzmusik meistens abspielt. Auf jeden dieser Bandpässe wird nun die Signalenergie gegeben. Der Bandpass, der sich daraufhin am meisten aufschwingt, hat dann offensichtlich am besten die richtige Geschwindigkeit getroffen.
Jetzt nochmal von vorne und im Detail - diesen Abschnitt gerne überspringen: Zuerst sammeln wir samples vom Mikrofon. Wir ziehen den gleitenden Durchschnitt ab, um ein Audiosignal zu erzeugen, welches um Null herum schwingt. Über jeweils ein chunk - eine Vierzigstelsekunde - summieren wir über quadrierte samples, um die Signalenergie in diesem chunk zu erhalten. Alles weitere passiert nun ebenfalls 40 mal die Sekunde. Wir geben die Signalenergie gleichzeitig auf alle Bandpässe - ebenfalls 40 an der Zahl - und schauen welcher davon sich am weitesten aufschwingt. Als relativen Amplitudenschätzer filtern wir die Absolutwerte aller Bandpassausgänge und setzen regelmäßig den Bandpass mit dem höchsten entsprechenden Wert auf aktiv. Nun haben wir das Problem, dass der Bandpass einmal pro beat schwingt, unsere gewollte Animation aber zwei beats benötigt. Wir müssen also irgendwie die Frequenz halbieren. Dafür verzögern wir das Signal um Pi/4 und schätzen mit der atan2-Funktion die Phase. Mit der bekannten Phase und einem einfachen Zustandsautomat konstruieren wir uns eine neue Phase, die nur halb so schnell steigt. Diese skalieren wir linear auf eine Sollposition des Maximums der Lichtwelle.
Wir wissen nun also zu jedem Zeitpunkt die Position des Scheitelpunktes der Lichtwelle. Die LEDs davor und dahinter werden ebenfalls angesteuert aber mit abfallender Helligkeit, so dass ein Verlauf entsteht. Die Maxima für den roten und blauen Kanal sind dabei gegenläufig verschoben, so dass ein räumlicher Farbverlauf entsteht.
Das Ganze ist hier illustriert: